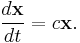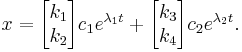Phase plane

A phase plane is a visual display of certain characteristics of certain kinds of differential equations; it is a 2-dimensional version of the general n-dimensional phase space.

Phase planes are useful in visualizing the behavior of physical systems; in particular, of oscillatory systems such as predator-prey models (see Lotka–Volterra equations). These models can "spiral in" towards zero, "spiral out" towards infinity, or reach neutrally stable situations called centres where the path traced out can be either circular, elliptical, or ovoid, or some variant thereof. This is useful in determining if the dynamics are stable or not.

Other examples of oscillatory systems are certain chemical reactions with multiple steps, some of which involve equilibria rather than reactions that go to completion. In such cases one can model the rise and fall of reactant and product concentration (or mass, or amount of substance) with the correct differential equations and a good understanding of chemical kinetics.

Certain systems of differential equations can be written in the form:

$\frac{d\bold{x}}{dt} = c\bold{x}.$

where c may be any combination of constants in order to create linear combinations with x on the right side; here x is in bold to indicate it is actually a vector, not a scalar.

Such systems may be solved algebraically (as seen here). More commonly they are solved with the coefficients of the right hand side written in matrix form using eigenvalues and eigenvectors. The eigenvalues represent the powers of the exponential components and the eigenvectors are coefficients. If the solutions are written in algebraic form, they express the fundamental multiplicative factor of the exponential term. Due to the nonuniqueness of eigenvectors, every solution arrived at in this way has undetermined constants c₁, c₂, and so on, up to the number of eigenvectors.

For the special case of a two-by-two matrix representing a system of differential equations, the solutions are:

$x = \begin{bmatrix} k_{1} \\ k_{2} \end{bmatrix} c_{1}e^{\lambda_1 t} %2B \begin{bmatrix} k_{3} \\ k_{4} \end{bmatrix} c_{2}e^{\lambda_2 t}.$

Here, $\lambda$ ₁ and $\lambda$ ₂ are the eigenvalues, and the two matrices containing (k₁, k₂), (k₃, k₄) are the basic eigenvectors. The constants c₁ and c₂ account for the nonuniqueness of eigenvectors and are not solvable unless an initial condition is given for the system.

The phase plane is then first set-up by drawing straight lines representing the two eigenvectors (which represent stable situations where the system either converges towards those lines or diverges away from them). Then the phase plane is plotted by using full lines instead of direction field dashes. The signs of the eigenvalues will tell how the system's phase plane behaves:

If the signs are opposite, the intersection of the eigenvectors is a saddle point.
If the signs are both positive, the eigenvectors represent stable situations that the system diverges away from, and the intersection is an unstable node.
If the signs are both negative, the eigenvectors represent stable situations that the system converges towards, and the intersection is a stable node.

The above can be visualized by recalling the behavior of exponential terms in differential equation solutions.

This page covers only the case for real, separate eigenvalues. Real, repeated eigenvalues require solving the coefficient matrix with an unknown vector and the first eigenvector to generate the second solution of a two-by-two system. However, if the matrix is symmetric, it is possible to use the orthogonal eigenvector to generate the second solution.

Complex eigenvalues and eigenvectors generate solutions in the form of sines and cosines as well as exponentials. One of the simplicities in this situation is that only one of the eigenvalues and one of the eigenvectors is needed to generate the full solution set for the system.

External links

Phase Planes and Solutions of Systems of Differential Equations

Phase plane

See also

External links